Главная » 2011 » Октябрь » 17 » Преобразование поверхности земного эллипсоида
19:33 Преобразование поверхности земного эллипсоида | |
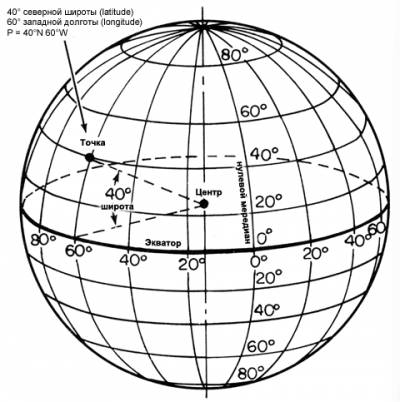
Ранее отмечалось, что топографические карты создают путем перехода от земного эллипсоида на плоскость соответствующей картографической проекции. Этот переход неизбежно сопровождается искажениями длин линий, площадей и углов, при этом эти искажения зависят от соответствующего математического алгоритма перехода. В одних проекциях можно избежать искажений площадей земельных участков, в других — искажений горизонтальных углов, но длины линий местности будут искажаться во всех картографических проекциях, кроме мест их расположения в отдельных точках или линиях, например, осевом меридиане зоны. Рассмотрим данный вопрос несколько подробней. При представлении результатов преобразования поверхности общего земного эллипсоида (тара) на плоскость, например в виде топографических и специальных карт, как правило получают уменьшенную математическую (или графическую) модель поверхности эллипсоида (шара). Степень уменьшения всей картографируемой поверхности показывает главный масштаб, который подписывают на карте. Ввиду наличия при соответствующих преобразованиях неизбежных искажений длин линий главный масштаб, в общем случае, сохраняется на карте только н отдельных точках или на некоторой линии карты. Если длина малого отрезка на поверхности эллипсоида (шара) равна S, а длина его изображения в картографической проекции равна Sг, то масштаб изображения т = Sг/S длины линии (отрезка) в картографической проекции будет выражен тем точнее, чем меньше значение S. При этом масштаб изображения, например в проекции Гаусса — Крюгера, в пределах одной и той же зоны различен и зависит от удаленности линии от осевого меридиана. Изменение масштаба обусловлено искажениями длин линий. Расчеты показывают, что наибольшие искажения получают те из них, которые находятся на краю шестиградусной зоны на широте экватора. На территории России относительное искажение длин линий в шестиградусной зоне достигает 0,00083, что не имеет практического значения при мелкомасштабном картографировании. Однако при создании крупномасштабных карт, например масштаба 1 ; 5000, такие искажения необходимо учитывать. По этой причине при крупномасштабном картографировании применяют трехградусные зоны. Искажения в длинах линий ведут к искажению площадей отображаемых фигур (земельных участков). Поправку Delta;Р в площадь Р земельного участка за переходе поверхности шара на плоскость в проекции Гаусса — Крюгера можно вычислить по следующей приближенной формуле: ΔP = P(Ym2/R2), е Ym — преобразованная ордината средней точки земельного участка, R = 6371 км. Расчеты показывают, что при удалении от осевого меридиана зоны на 100 км и площади земельного участка, равной 1000 га, поправка ΔP = 0,25 га, а при удалении на 200 км эта же поправка будет равна 0,98 га. При отображении сведений о пространственном положении земельных участков важен выбор картографической проекции, обеспечивающей принятие оптимальных решений. Выбор конкретного вида картографической проекции зависит от многих факторов: географического положения изображаемой территории, ее размеров и формы (конфигурации), степени показа смежных с картографируемой областью территорий и др. При выборе картографической проекции необходимо учитывать назначение и специализацию, а также масштаб и содержание карты; состав и содержание задач, которые будут решать с ее использованием и пр. Немаловажное значение при этом имеет характер искажений и возможность их учета при решении практических земельно-кадастровых задач. Для изображения пространственного положения земельных участков и иных объектов недвижимости, расположенных на небольших территориях, часто используют ортогональные картографические проекции — изображение пространственного объекта местности (части земной поверхности) на плоскости посредством проектирующих лучей, перпендикулярных к плоскости проектирования. В качестве них, как правило, служат отвесные линии. При этом уровенную поверхность в пределах картографируемой территории принимают за плоскость, а отвесные линии — перпендикулярными к ней. В результате соответствующих преобразований получают ортогональную проекцию изображенной на плоскости части земной поверхности. Заметим, что ортогональную проекцию длины линии (отрезка) местности на горизонтальную плоскость называют горизонтальным проложением, а соответствующее картографическое произведение —топографическим планом местности. План местности характеризуется основными свойствами: расстояния на плане пропорциональны горизонтальным проложениям линий местности; горизонтальные углы с вершиной в любой точке плана равны соответствующим горизонтальным углам на местности; масштаб плана есть величина постоянная и равная отношению длины отрезка на плане к его горизонтальному проложению на местности. Установим размеры земельного участка, поверхность которого можно считать плоской, а не сферичной. Допустим, что Земля представляет собой шар радиусом R, на поверхности которого расположены две точки А и В. Проведем касательную к поверхности шара в точке А и одновременно перпендикулярную к направлению радиуса шара в этой точке. Обозначим дугу, стягивающую точки А и В в виде AB, a проекцию этой дуги на плоскость — через Sab . Тогда разность ΔS. равная ΔS = SAB - AB, будет ни что иное, как искажение длины дуги при ее отображении на плоскости. Замена длины дуги земной поверхности ее проекцией на плоскости Для рассматриваемого случая значение ΔS определим по следующей приближенной формуле: ΔS = 0,3 (AB3/R2). Для дуг различной длины абсолютные ΔS и относительные ΔS /AB значения расхождений следующие. При расчетах принимают радиус шара R = 6371 км. При решении подавляющего числа земельно-кадастровых задач, основанных на использовании топографо-геодезических данных, значением относительного искажения длин линий менее 1 :1 000 000 можно пренебречь. На основании этого можно сделать вывод, что в качестве картографической проекции при отображении участка земной поверхности размером менее 10 км2, а в условиях равнинного рельефа менее 20 км2 можно выбрать ортогональную картографическую проекцию. Другими словами, необходимая картографическая информация для решения соответствующих земельно-кадастровых задач в этом случае может быть получена на основе использования топографического плана. | |
|
| |
Полезная информация:
При полном или частичном использовании материалов гиперссылка обязательна.
| Форма входа |
| Календарь | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Категории раздела | |||||||||||||||||
|
| Поиск |
| Статистика |
| Природа Урала |
|