Обратная геодезическая задача.

Дано: Из прямоугольного
XA; YA треугольника АВС
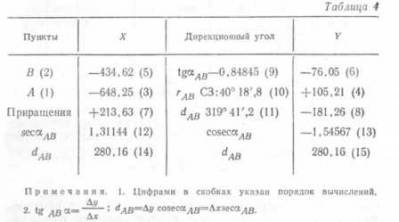
XB; YB имеем:

1. X = XB – XA; Y = YB – YA; АВ - ? ; SАВ - ?
2. tg (rАВ) = ΔY : ΔX ;
3. rАВ = аrctg(rАВ);

Для вычисления румба в градусной мере необходимо выполнить на микрокалькуляторе следующие операции:
делением ΔY на ΔX находим tg(rАВ), далее нажимаем клавиши 2ndF и tan над которой стоит символ (tan-1), получаем значение румба в градусах, желательно до семи знаков после запятой. Для перевода румбического значения в градусы минуты секунды (° ´ ´´) необходимо нажать клавишу 2ndF и клавишу DEG над которой стоит символ (D.MS ). Название румба определяется в зависимости от того в какой четверти находится данная линия. Четверть определяется по знакам
ΔY и ΔX.

4. Дирекционный угол линии АВ (αАВ) вычисляется с учётом четверти, в которой находится данная линия, а четверть определяется по знакам приращений координат (ΔX , ΔY).

5. Формулы для вычисления дирекционного угла линии по румбу

Первая четверть: αАВ = rАВ ; (название румба СВ)
Вторая четверть: αАВ = 180° - rАВ; (название румба ЮВ)
Третья четверть: αАВ = 180° + rАВ; (название румба ЮЗ)
Четвёртая четверть: 360° - rАВ; (название румба СЗ)

6. S(AB)= ΔX : Cosα(АВ) ;
7. S(AB)= ΔY : Sinα(АВ) ;
8.
9. SAB ср. вычисляется, как среднее из трёх полученных значений расстояния АВ.
Пример.
Дано: Решение:
XA = 28359.109 м 1. X = XB – XA=29007.458 – 28359.109 = 648.349м.
YA = 29408.251 м 2. Y = YB – YA=29903.074 – 29408.251 = 494.823м.
XB = 29007.458 м 3. tg (rАВ) = ΔY : ΔX = 0.7632047;
YB = 29903.074 м 4. rАВ = СВ : 37˚ 21´ 03.´´8 ;

5. АВ = 37˚ 21´ 03.´´8 ;
АВ - ? ; SАВ - ?
6. S(AB)= ΔX : Cosα(АВ) = 815.602 ;

7. S(AB)= ΔY : Sinα(АВ) = 815.602 ;

8. = 815.602 ; 9. SAB ср. = 815.602 ;